Maître de Conférences, Faculté des sciences, Université de Montpellier
Address :
IMAG - UMR 5149 - c.c. 051
Université de Montpellier
Place Eugène Bataillon
34090 Montpellier, France
ORCID
ArXiv
Where can you find me ? Office 219, building 9, campus map
Since septembre 2022, I am maître de conférences in the team GTA (Geometry, Topology and Algebra) at IMAG. My research field is Algebraic combinatorics (une courte présentation ici).
Je suis membre élue de la commission RH et du conseil du pôle MIPS depuis janvier 2023. Je fais partie du bureau du GDR Homotopie depuis Janvier 2023. Je suis responsable du GT CombAlg du GDR IM avec Viviane Pons et Vincent Pilaud.
From 2017 to 2022, I was maître de conférences in the teams "combinatoire" (combinatorics) and "algèbre et calcul" (algebra and computation) at IRIF. I was head of this last team from November 2020 to June 2022. A quick overview of this team is available here.
Previously, I had a 2-year CIMI postdoctoral position in the team mathématiques fondamentales (fundamental mathematics) of the Institut de Mathématiques de Toulouse.
I defended my thesis on November, 21st 2014, entitled "Hypertrees and Semi-pointed partitions" under the supervision of Frédéric Chapoton. Here is the manuscript (in french, version of January 2015) and here is the beamer.
Nouvelles
Deux nouvelles sections sont en cours d'ajout sur le site : Crochet et Grrrls ! N'hésitez pas à aller y faire un tour !
Un sujet de stage de M2 est disponible ici.
Dernière mise à jour / Last update: 03/08/23.
Recherche / Research
Ma recherche se situe en combinatoire algébrique. La combinatoire est l'étude de structures discrètes, c'est-à-dire d'objets que l'on peut énumérer. Par exemple, des cailloux, des arbres, des partitions... par opposition aux objets continus comme de l'eau ou du temps (exactement la même différence qu'entre "how many" et "how much" en anglais).
La combinatoire algébrique est l'étude de structures algébriques sur ces objets discrets comme des ordres partiels ou des produits. Ces structures donnent un moyen de "dévisser" les objets pour mieux les comprendre. De manière imagée, imaginez que vous vouliez étudier l'ensemble des constructions possibles en lego : ce serait vraiment difficile parce qu'il y en a beaucoup. Une manière plus efficace serait de se fixer un ensemble de brique donnée et des règles de construction : par exemple, je pars avec 5 briques lego de taille 2 par 4 et je préfère les emboîter de manières à ce que deux briques emboitées partage 4 petits ronds. Ajouter ces règles, ces "structures", permettent de dire des choses plus précises, d'exhiber des propriétés (par exemple, je n'arriverai pas à construire un carré de longueur impaire).
Est-ce des maths ou de l'informatique ? Quand on s'intéresse à une plante respire, est-ce de la biologie ? de l'horticulture ? de la chimie ? Les structures discrètes sont au coeur des structures de données informatique et des algorithmes. Tout dépend après des lunettes avec lesquelles on les regarde (et j'aime bien pour ma part en changer régulièrement!).
Un exposé grand public présentant ma recherche est disponible ici. Un exposé de présentation à mes collègues montpelliérains est disponible ici.
Mots clés :
Combinatoire algébrique, Topologie algébrique, Posets, Opérades et Espèces, Cohomologie, Hyperarbres, Partitions, Bigèbres généralisées, Représentations du groupe symétrique, Loi distributive...
Projets / Projects
Je suis actuellement porteuse du projet PEPS JCJC INSMI PATTAPO, portant sur l'étude des arbres de parking.
Je fais partie des ANR suivantes- 2021-2025 : ANR Higher Algebra, Geometry and Topology (HighAGT), portée par Bruno Vallette
- 2021-2025 : ANR Carplo , portée par Jean-Yves Thibon
- 2021-2025 : ANR JCJC S3, portée par Christine Tasson
- 2019-2023 : ANR JCJC ALCOHOL, portée par Pierre-Louis Giscard
J'ai porté en 2019 le projet Peps CoLA INS2I (Combinatorics of Lattices and Applications), portant sur la conjecture d'évasivité.
Évènements / Conférences
J'ai co-organisé ou je co-organise actuellement
- Winterbraids XIII qui aura lieu en février 2024
- la rencontre annuelle du GT combalg en juillet 2023
- la Master class Homology of groups and functors en juin 2023
- SOCS 2020 (soutenue par le DIM RFSI)
- Inter'actions 2014
Responsabilités
- Depuis Juin 2023 : responsable du GT CombAlg du GDR IM
- Depuis Janvier 2023 : membre élu de la commission ressource humaine et du conseil de pôle MIPS de l'université de Montpellier
- Depuis Janvier 2023 : membre du bureau du GDR Homotopie et applications
- Novembre 2020-juin 2022 : responsable de l'équipe "Algèbre et Calcul".
- 2019-2022 : membre élu du CS de l'UFR d'Informatique, en binôme avec Christine Tasson, puis Jean-Krivine.
- 2018-2022 : co-organisatrice de la fête de la sciences
- 2012-2013 : responsable du séminaire des doctorants.
Encadrement
J'ai encadré les stages suivants:- Louis Belle, M2 Mathématiques, "Nombre de Moebius du treillis de Tamari", 2023
- Hélène Han, L3 Mathématiques, "Order de Tamari sur les partitions non croisées", 2022
- Alexandre Nizard et Adib Bennasser, L3 Informatique, "Planche de Galton et arbres binaires plans", 2022
Publications :
Pré-publications / Preprints
Generalised mixed distributive laws and Hopf-Borel type theorem for operads
E. Burgunder & B. Delcroix-Oger
ArXiv
An operad is never free as a pre-Lie algebra
E. Burgunder, B. Delcroix-Oger & D. Manchon
ArXiv
Polydendriform structure on faces of hypergraph polytopes
P.-L. Curien, B. Delcroix-Oger & J. Obradovic
ArXiv
A spoonful of dendrology : from hypertrees to Cayley trees
Tridendriform structures on faces of hypergraph
associahedra
Tridendriform structures on faces of hypergraph
associahedra
Cellular diagonals of permutahedra
B. Delcroix-Oger, M. Josuat-Vergès, G. Laplante-Anfossi, V. Pilaud & K. Stoeckl
ArXiv (soon)
De la diagonale du permutoèdre aux arbres k-colorés : une histoire de partitions et d'arbres
Operadic posets and their cohomology
B. Delcroix-Oger & C. Dupont
ArXiv (soon)
Hypertrees, postLie and pre-Lie operads
B. Delcroix-Oger & C. Dupont
ArXiv (soon)
Poset homology and operads
From pre-Lie to post-Lie operads through hypertrees
Mini-cours Posets, Incidence Hopf algebras and operads (partie 1, 2, 3 et 4, versions annotées : 1, 2 et 4)
Articles parus dans des journaux avec comité de lecture :
Action of the symmetric groups on the homology of the hypertree posets
B. Oger
J. Algebr. Comb. 38, No. 4, 915-945 (2013)
DOI, ArXiv
Decorated hypertrees
B. Oger
J. Comb. Theory, Ser. A 120, No. 7, 1871-1905 (2013).
DOI, ArXiv
Incidence Hopf Algebra of the Hypertree Posets
B. Oger
Sémin. Lothar. Comb. 72(2014-2015), B72d, 22 p. (2015)
Journal, ArXiv
Semi-pointed partition posets and Species
B. Delcroix-Oger
J. Algebr. Comb. 45, No. 3, 857-886 (2017).
DOI, ArXiv
Structure theorems for dendriform and tridendriform algebras
E. Burgunder & B. Delcroix-Oger
Chapoton, Frédéric (ed.) et al., Algebraic combinatorics, resurgence, moulds and applications (CARMA). Volume 1. Berlin: European Mathematical Society (EMS). IRMA Lect. Math. Theor. Phys. 31, 19-66 (2020).
DOI, version 0.99
Non-ambiguous trees: new results and generalisation
J.-C. Aval, A. Boussicault, B. Delcroix-Oger, F. Hivert & P. Laborde-Zubieta,
Eur. J. Comb. 95, Article ID 103331, 28 p. (2021).
DOI
Operads with compatible CL-shellable partition posets admit a Poincaré-Birkhoff-Witt basis
J. Bellier-Millès, B. Delcroix-Oger & E. Hoffbeck,
Transactions of the AMS 374, No. 11, 8249-8273 (2021).
DOI , ArXiv
Some properties of the parking function poset
B. Delcroix-Oger, M. Josuat-Vergès & L. Randazzo,
Electron. J. Comb. 29, No. 4, Research Paper P4.42, 49 p. (2022)
DOI
Parking trees , Arbres de stationnement , Parking trees
Articles parus dans des conférences :
Prelie-decorated hypertrees (FPSAC 2013)
B. Oger
Proceedings of the 25th international conference on formal power series and algebraic combinatorics, FPSAC 2013, Paris, France, June 24–28, 2013. Nancy: The Association. Discrete Mathematics & Theoretical Computer Science (DMTCS). Discrete Mathematics and Theoretical Computer Science. Proceedings, 445-456, electronic only (2013).
Link
Hyperarbres décorés et codes de Prüfer
B. Oger
publication du Forum des jeunes mathématicien-ne-s (2013)
Texte
Semi-pointed partition posets (FPSAC 2015)
B. Delcroix-Oger
Proceedings of the 27th international conference on formal power series and algebraic combinatorics, FPSAC 2015, Daejeon, South Korea, July 6–10, 2015. Nancy: The Association. Discrete Mathematics & Theoretical Computer Science (DMTCS). Discrete Mathematics and Theoretical Computer Science. Proceedings, 321-332 (2015).
Non-ambiguous trees : new results and generalisation (FPSAC 2016)
J.-C. Aval, A. Boussicault, B. Delcroix-Oger, F. Hivert & P. Laborde-Zubieta
Proceedings of the 28th international conference on formal power series and algebraic combinatorics, FPSAC 2016, Vancouver, Canada, July 4–8, 2016. Nancy: The Association. Discrete Mathematics & Theoretical Computer Science (DMTCS). Discrete Math. Theor. Comput. Sci., Proc., 83-94 (2020)
DOI , ArXiv
Some Properties of the Parking Function Poset (FPSAC 2020)
B. Delcroix-Oger, M. Josuat-Vergès & L. Randazzo,
Sémin. Lothar. Comb. 84B, Article 59, 12 p. (2020).
DOI
Articles de médiation :
"Mathématiques du crochet et crochet mathématique", Au Fil des Maths n° 537 Mathématiques et arts, 2020
Article
Autres documents de recherche :
Thèse intitulée "Hyperarbres et Partitions semi-pointées : Aspects combinatoires, algébriques et homologiques", dirigée par F. Chapoton (ICJ), soutenue le 21 novembre 2014
Etude de séries particulières dans le groupe des séries en arbres , dirigé par F. Chapoton (ICJ)
Les transpositions musicales et autres transformations de la gamme, dirigé par M. Andreatta (IRCAM)
Exposés donnés / Talks :
Poset homology and operads, LHC days 2023, june 2023, IRIF, Paris
La recherche dans un laboratoire de mathématiques : fonctions de Parking, journée "Filles, Maths et Informatique : une équation lumineuse", vendredi 14 avril 2023, Montpellier
De la diagonale du permutoèdre aux arbres k-colorés : une histoire de partitions et d'arbres, journées du GDR IM, vendredi 7 avril 2023, IRIF, Paris
From pre-Lie to post-Lie operads through hypertrees, conférence Alpe, march 2023, Montpellier
Enseignements :
J'enseigne actuellement en licence d'informatique et en licence et master de mathématiques à la faculté des sciences de l'Université de Montpellier.
J'ai obtenu en 2019 le Prix de l'innovation pédagogique numérique de l'université de Paris, avec mes collègues Antonio Bucciarelli, Sophie Laplante et Christine Tasson, pour un projet de tableau interactif numérique. Ce projet, réalisé dans le cadre de mon parcours de formation MCF, a donné lieu à un mémoire validé par le certificat CertifiENS délivré par SAPIENS.
Matériel pédagogique :- Cours de Mathématiques discrètes pour les L3 informatique (version de 2019)
Une partie de l'évaluation portait sur la rédaction d'un article de blog - Première partie du cours d'introduction à Java pour les L1 informatique ayant fait NSI au lycée
- TD 1 du cours de M2 de combinatoire du MPRI.
- Mini-cours Posets, Incidence Hopf algebras and operads niveau M2/doctorat (partie 1, 2, 3 et 4, versions annotées : 1, 2 et 4)
Réalisations logicielles :
Contributions SageMath
- Arbres de parking (avec poset) , développé dans le cadre du projet PEPS JCJC INSMI PATTAPO
- Ticket 19446
- Hyperarbres et hyperarbres pointés (avec poset)
- Partitions semi-pointées (type A) (avec poset)
- Partitions semi-pointées de type B (avec poset)
Projets
Médiation scientifique :
Le partage de cet amour de la science qui m'anime est pour moi essentiel. J'encadre tous les ans des stagiaires de 3ème : n'hésitez pas à me contacter si vous êtes intéressé.e.s !
Réalisations
- Encadrement de deux groupes de 4e-3e pour le stage MAthC2+ de février 2023 de l'IREM, thèmes : surfaces hyperboliques
Réalisations d'un des groupes en pâte fimo:
-
Réalisation de surfaces au crochet (atelier fête de la science)
Exposés
- La recherche dans un laboratoire de mathématiques : fonctions de Parking, journée "Filles, Maths et Informatique : une équation lumineuse", vendredi 14 avril, Montpellier
- Présentation "Paroles de chercheurs et de chercheuses" présentée le 19 janvier 2022 au lycée Louis-le-Grand.
Article
Article de médiation : "Mathématiques du crochet et crochet mathématique", Au Fil des Maths n° 537 Mathématiques et arts, 2020Fête de la science
J'ai animé pendant 4 ans la fête de la science de l'UFR d'Informatique de l'Université Paris Diderot, puis Paris Cité. La page associée est visible ici. L'une de nos interventions à la Fête de la science 2020 au collège Alain Fournier a fait l'objet d'un article. Une partie du matériel utilisé est disponible ci-dessous:- Atelier tresse (fiche pour les animateurs, nécessite le matériel physique)
(photo Sandrine Cadet)
- Atelier Tours de Hanoi (fiche par Léo Planche)
- Atelier Codage de César (fiche par un ATER UP7)
- Atelier Bits de parité (fiche par Pierre Cagne)
- Atelier codage binaire (matériel)
- Atelier Anniversaire (matériel, fiche réalisée avec Sandrine Cadet et Valia Mitsou)
- Protocole zéro-connaissance (fiche 1, fiche 2 )
Crochet :
!!!!! Section en construction !!! Cette section contient les diagrammes pour faire les principaux polygones- Triangle
- Carré
- Pentagone
- Hexagone
- Octogone
Illustration de la bannière: Nadja Buttendorf, Soft Nails ~ ♥[ASMR] Kleincomputer Robotron KC87 ♥, videostill, Photo de l'exposition Computer Grrrls à la Gaîté Lyrique
Grrrls !
Quelques pointeurs sur les femmes et les mathématiques / informatique :- la magnifique exposition "Computer grrrls" organisée à la Gaîté Lyrique en 2019, et sa frise chronologique
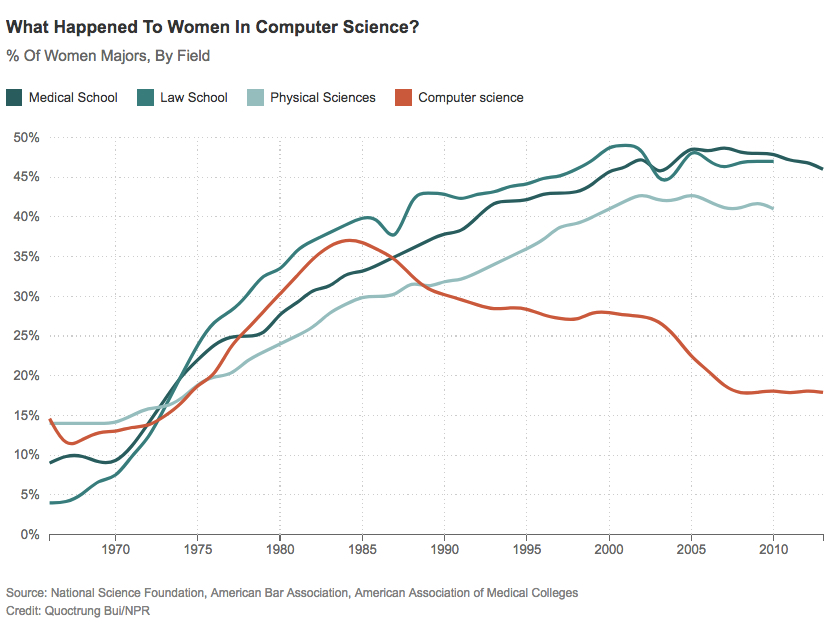
- L'évolution des effectifs féminins à l'université en math : les mathématiques fondamentales (ou pures) est la discipline la moins féminisée à l'université (13,8% de femmes). Le nombre de femmes professeur des université et maître de conférences a baissé chaque année entre 1996 et 2020 et atteindra 0 en 2060 pour les professeurs et 2064 pour les maîtres de conférences si rien ne change. Le taux de femmes en informatique est plus élevé (24,2%), mais est-ce vraiment bon signe au regard du graphique ci-dessous ?
